This document describes the changes made to my old programs FLATNOSE.EXE and TPRFLTNS.EXE to bring them up to more-or-less the level of the pointed-nose program M79APCLC.EXE. They are also Microsoft QuickBASIC 4.5 text-only BASIC programs like their predecessors and require the BRUN45.EXE support program be in the same folder as the main program.
To run under the new WINDOWS 7 Operating System, which no longer supports non-Microsoft MSDOS programs, they require the shareware application programs DOSBox (currently at Version 0.74) to create an MSDOS "sandbox" Window in which most MSDOS programs will run (my text-based programs work fine here) and DOSShell (currently at Version 1.7) which automatically starts an instance of DOSBox and runs the selected MSDOS program inside it - this last program can be replaced by one of several other pseudo-WINDOWS icon-based MSDOS-library programs that run with DOSBox, but this one works well for me and is intuitive.
The reason for the revisions is that I obtained a set of tests with carefully-made 20mm flat-nosed cylindrical projectiles fired against a modern high-tensile steel called WELDOX 460, which had an average Ultimate Tensile Strength of 81,200 pounds/square-inch (psi), which caused samples to tear in two pieces when slowly pulled apart, compared to 115,000 psi for average WWII US Navy Special Treatment Steel (STS). These WELDOX 460 results were at right-angles ("normal" or zero-degrees obliquity) only, but showed a number of added features concerning my previous set of tests used with my original flat-nose program. Those were exclusively based on tests with US Navy WWII STS of 0.5-3" thickness (0.167-1.0-caliber) fired on by US Army WWII 15-lb 76.2mm (3") M79 Armor-Piercing (AP) Shot projectiles which had had their noses sliced off flat, reducing their weight to 10-11 pounds, and with a few specially-made 3" 15-lb flat-nose AP shot projectiles, at obliquities of 0 to 75 degrees.
The US Navy WWII tapered-flat-nose projectile tests were against standard STS too with a set of specially-made 3" 13-lb uncapped Common Projectiles (same as US Army "APHEBC Shells") with a thin conical windscreen (not used in the armor tests), a conical taper to 1.425" nose-height above the cylindrical body upper edge (0.475-caliber) and a flat nose width of 2.55" (0.85-caliber), including the small narrowing due to the cutting of the threads to hold the windscreen into the upper edge of the flat nose. It was tested using STS plates 0.5-2" thick at 0-75-degrees obliquity angle.
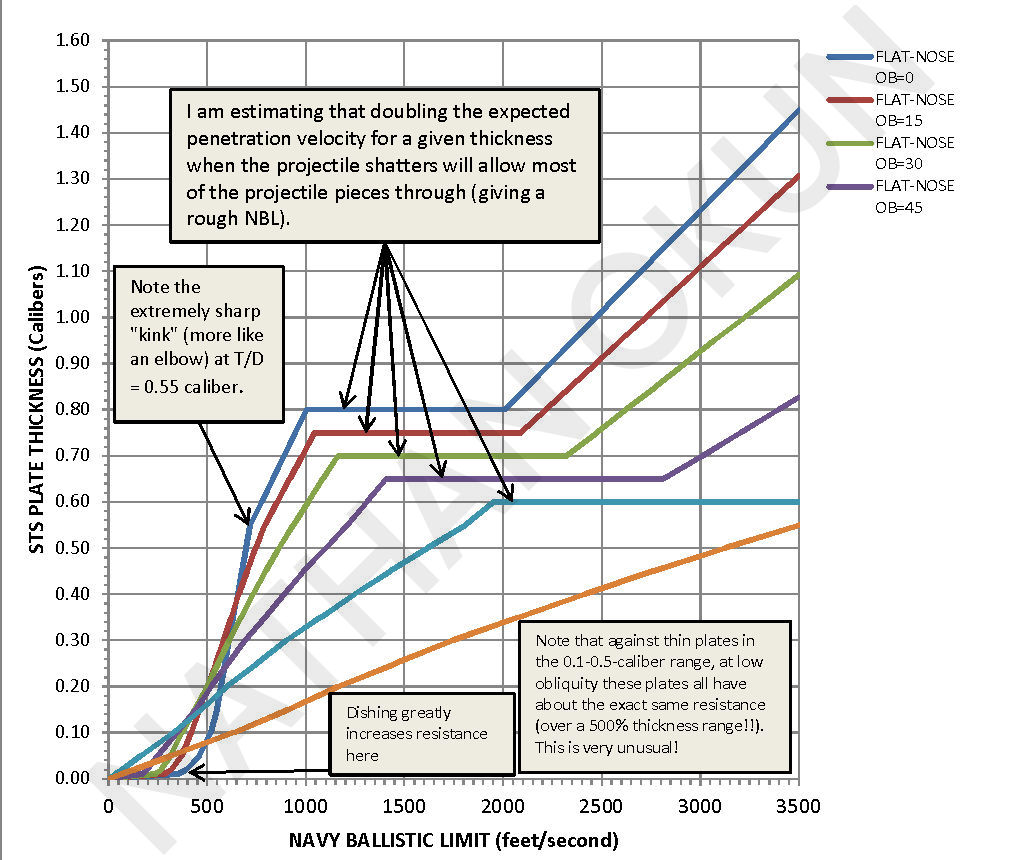
The STS tests had the projectile hitting at normal shattering at impacts with STS plate of close to 2.4" (0.8-caliber), but only slightly deforming against plates just under that thickness at circa 2.25" (0.75-caliber). The WELDOX 460 test projectiles shattered against any plate over 20mm (1.0-caliber) in thickness, but remained undamaged against all thinner plates, no matter how high the striking velocity was raised. Increasing the striking velocity by 50% over the projected non-shatter Navy Ballistic Limit (NBL - complete penetration with nil remaining velocity after penetration) did not penetrate the thicker, shatter-causing plates or even increase by much the depth of the widened, irregular pit in the plates, so I am estimating at least doubling the extrapolated non-shatter velocity is needed to give the shattered NBL (with most, but not all, projectile pieces penetrating, of course). This is just an educated guess, of course. I made the rough estimates that at normal obliquity, it takes a 0.8-caliber-thick STS plate to shatter a high-quality flat-nose projectile, 1.05-caliber-thick HTS, 1.15-caliber-thick Mild Steel, and 1.25-caliber-thick wrought iron. This is modified by the linear 75% formula stated above. For a tapered-flat-nose projectile I am making a rough guess that the normal-obliquity shatter thickness goes up with the inverse of the ratio of the flat area to that of a full-flat-nose plate. Thus, the 13-lb test projectiles with an 85% flat nose diameter had a 72.25% flat area, so the normal-obliquity shatter thicknesses given for a full-flat-nose go up by 1/0.7225 = 1.38408 and the normal-obliquity shatter thickness for the tapered-flat-nose projectile against STS is 0.8 x 1.38408 = 1.1073-caliber, decreasing in a straight line with the obliquity angle in degrees to 75% of that thickness at 60 degrees obliquity and over. Ditto for the other kinds of steel.
These programs also now compute the Exit Angle and Remaining Velocity of the Projectile after penetration and the Direction of Motion and Weight and Velocity of the armor plug ejected from the plate back (flat noses act like cookie cutters), using a combination of the formulae from both M79APCLC.EXE and FACEHD68.EXE. As a convenience feature, they also will only display the NBL calculated for a given plate type at a given obliquity (and the NBL of the STS standard for comparison), allowing a minimum thickness, maximum thickness, and a thickness step to create a table of multiple values in one go. The rest of the outputs are discarded in this alternate output selection.
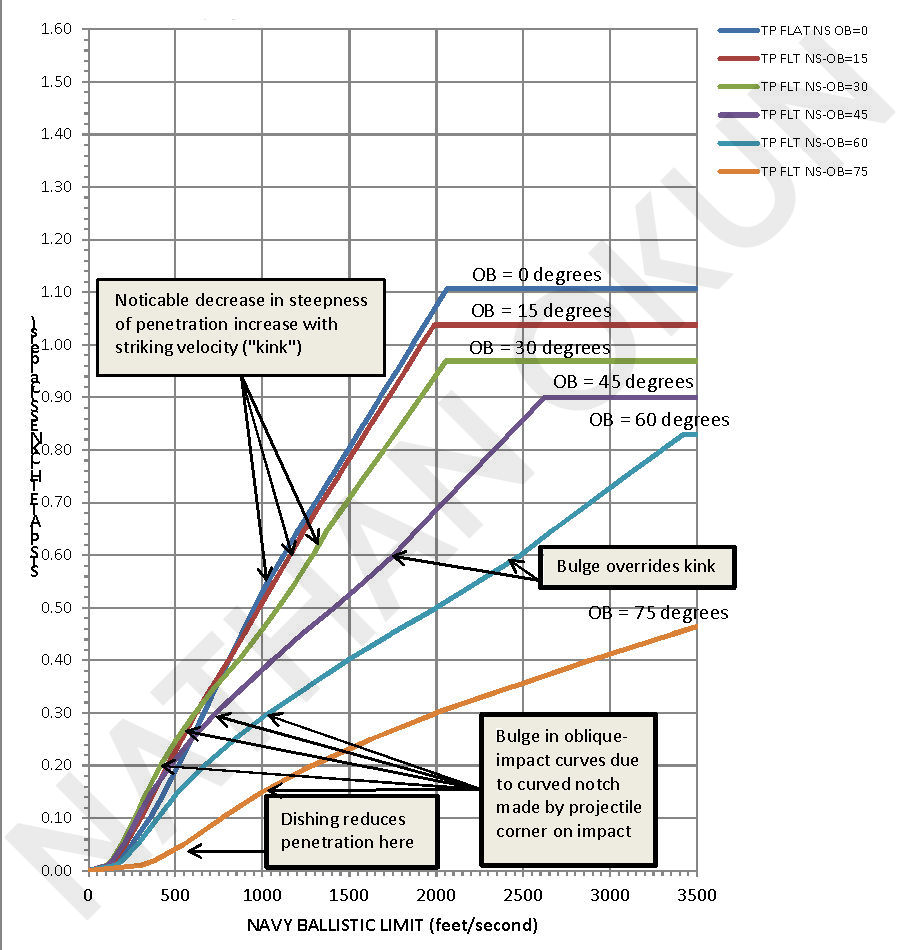
I sent to NAVWEAPS.COM my FLATNS20.EXE program, which was also based on both the 20mm tests and the 3" tests, M79APCLC.EXE, and FACEHD68.EXE. It changed the curved penetration thickness versus striking velocity plots to straight lines. This was due to the normal-obliquity WELDOX 460 tests giving such a straight line with a sharp "kink" or "elbow" at a plate thickness of 0.55-calibers, just like I had found with my 3" vs STS flat-nose tests, though I had put smooth curves through the points, not straight lines. For normal impact, there is indeed a straight-line (linear) relationship between penetration and striking velocity (T = KV, roughly), since the projectile is be resisted by the entire plate thickness in all cases from the initial instant of impact until the plug is punched out and the projectile can proceed forward against the friction-only resistance along its side. This means that penetration is T = KV to a good first approximation because the Projectile Kinetic Energy = .5 x M x V2 and the Energy ("Work") Needed To Penetrate a Plate of Thickness T = T x (K x T) = KT2, where K x T is the resistance force of a plate of thickness T with a fixed average resistance K per unit plate thickness (length) around the edge of the hole and the projectile must move the entire distance T against this force to eject the plug and to penetrate. These are equal at the NBL. This kind of resistance is the opposite from the case, as with a thick plate being penetrated by a pointed projectile, where the nose is only being resisted by the metal immediately in front of it and to its sides, as if it was swimming in water, so the energy used per unit depth penetrated is roughly constant for every increment of thickness, not dependent on the total plate thickness. In that case the penetration is at the square of the striking velocity. This means that the penetration is roughly T = KV2. Most moderately-thick ductile armor hit by pointed and oval-nosed projectiles acts in-between these extremes, hence the rather good agreement with T = KV1.43 used by the DeMarre Nickel-Steel Penetration Formula for these thicknesses (it does not work for very thin or very thick plates or for anything but normal obliquity).
I applied this straight line revision to all impact obliquities in FLATNS20.EXE, but analysis of the tapered-flat-nose data while revising that program to TPFLNS20.EXE showed that the straight-line approximation did not completely apply to impacts at other obliquities for the thinner plates under that kink thickness of 0.55-caliber. This is due to dishing (wide-area denting of the plate around the impact point), which decreases to a minimum with the full-flat-nose projectile at T = 0.55-caliber (circa 0.6-caliber for the tapered-flat-nose projectile). This dishing increases the resistance of the projectile hitting thin plates by acting like a trampoline. Thus, the effects get less and less as obliquity goes up and the forces on the plate get more and more along the plate face, not into the plate face, as I showed in FLATNS20.EXE. But there is also a secondary effect that causes dishing to make penetration EASIER for a full-flat-nose or tapered-flat-nose projectile. As the corner of the edge of the nose (the "chin") digs into the plate, it dishes in a "V" shape, so the "smiley-face notch" made by the chin bends the armor material sharply downward just in front of the chin, decreasing the impact obliquity somewhat and thus reducing the resistance somewhat (a "shot trap"). This effect decreases when dishing decreases against thicker plates or when it has little effect against very thin plates, which tear open easily anyway. Thus, we get a bulge in the otherwise straight-line relationship for thin plates at oblique impact, where the penetration ability at a given striking velocity increases a few percent in the center (circa 0.3-0.4-caliber thickness), decreasing the NBL, and this change drops to zero against both very thin and circa-half-caliber-and-up plates. Therefore, the curves I originally recorded for full-flat-nose projectile at oblique impact against under-half-caliber STS plate were correct. I had swung the pendulum too far in the straight-line-only computation direction and had to move back toward the center, hence the need for FLATNS21.EXE and further improvements in FLATNS30.EXE. My aim is to be as correct as possible, no matter how much extra work it entails!
Using the information concerning the linear decrease in the shatter thickness with increasing obliquity given by Dr. Allen V. Hershey, head of the Ballistic Calculations Branch of the WWII US Naval Proving Ground, Dahlgren, Virginia, USA, in his discussions of AP cap shatter, wherein the thickness needed to shatter a hard AP cap dropped in a straight line with increasing obliquity angle from its maximum at normal to a minimum at 60 degrees obliquity and remained at that thickness for all higher obliquities, I estimated that a similar linear drop in the required thickness would be to 75% of the normal-obliquity thickness at 60 degrees and up since no flat-nose projectile hitting an STS plate obliquely shattered even when tested at up to 1.5" (0.5-caliber) plate thickness, so the drop cannot have been much more than this estimate. I adopted this drop-off rate for both flat nose and tapered flat nose projectiles in my new programs.
I now had for my full-flat-nose database two different plate types, two different plate thickness ranges, two different projectile diameters, and two different projectile weights (the 20mm (0.7874") projectiles weighed 0.4343-lb, making them far heavier than the M79-type projectiles in proportion to their size). I assumed that (1) the scaling term used for the M79APCLC.EXE pointed projectiles against STS also worked for these flat-nose and tapered-flat-nose projectiles against all ductile iron and steel armors (and even with non-steel materials) and (2) that the ratio of plate qualities was roughly in proportion to their respective tensile strengths, where 81.2/115 = 0.71, so I chose as a first chop a conservative Plate Quality Factor (QA) of 0.75 for the WELDOX 460 plate compared to STS, which more-or-less matched my old HTS-to-STS QA for WWI and WWI armors and construction steels. These assumptions seemed to work fine when I made a change to only the formula that adjusted the effect that the different projectile weights had on penetration (the effects were different for a full-flat-nose projectile from the M79 pointed projectile to give the correct NBL values for both 20mm and 3" flat-nose data sets, but this was to be expected, as my FACEHD68.EXE program, which also punched out plugs of armor, had this value quite different from the M79APCLC.EXE value). For the tapered-flat-nose program, which was also against WWII US Navy STS, I split the difference between these two extremes for its weight term.
This weight change effect function is interesting. For M79-type pointed projectiles, the penetration thickness is T = R x (W x V2)p, where R is the resistance for a given narrow thickness range (it varies with thickness and obliquity and projectile nose shape, over a limited range of nose shapes) and p is the adjustment factor for the kinetic energy in that thickness range (it also varies with thickness and nose shape, but not with obliquity). The variation in resistance is still a function to the entire projectile kinetic energy (0.5 x M x V2), where the projectile weight W is always a fixed ratio to its mass M. The value for p = 0.7143 is for all plate thicknesses in the DeMarre Formula, for example. For the full-flat-nose projectile, which has p = .5 when it applies to V, giving, as mentioned, close to 2 x .5 = 1 as the power to V (plus the small curve adjustment for thin plates under 0.5-caliber), instead of the exponent of W being p = 0.5 (if the full kinetic energy of the projectile were used during the penetration), the p used for the weight term is smaller at 0.381145. It implies that the nose weight of the projectile gets more involved in punching through the plate using impact-initiated shearing than the middle and lower portions of the projectile do, only after which the weight of the base of the projectile merely piles on to increase the remaining velocity of the plate pieces and projectile after the impact. This is not as extreme as the weight's p-value of 0.2 for face-hardened armor (where only the upper end of the projectile has any real effect at all prior to the hard, brittle face suddenly failing by cracking through), but it does show that most of the penetration is done by the front end of the projectile and the weight near the base is only on "cleanup" after the plug has been sheared out of the plate. For the tapered-flat-nose program, I use a value of p for the weight term in the middle, giving p = .6895. This is significantly closer to the M79-type pointed nose, implying that the ring of material, which accounts for 100 - 72.25 = 27.75% of the mass of the plate being moved away from the projectile path - which has to be displaced forward and sideways relatively gradually after the central plug is ejected to let the projectile through the plate - now requires the full mass of much more of the projectile middle and lower body, though this is still not as though it was a gradual process over the entire penetration time.
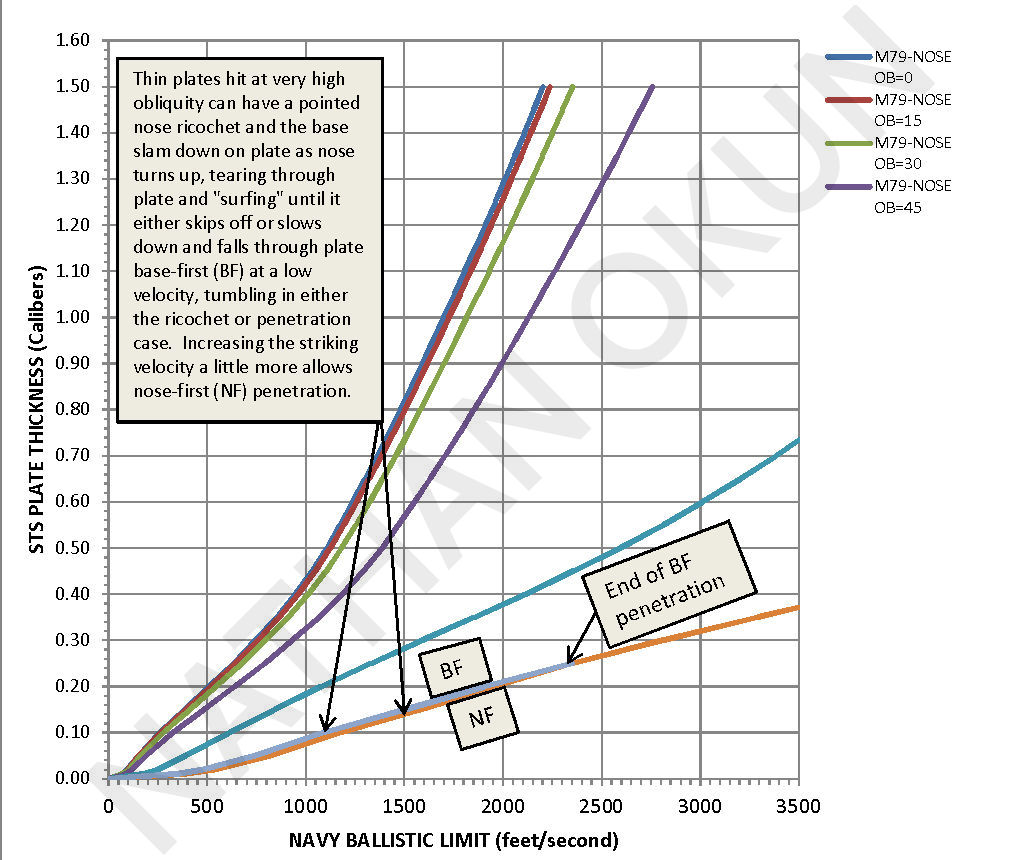
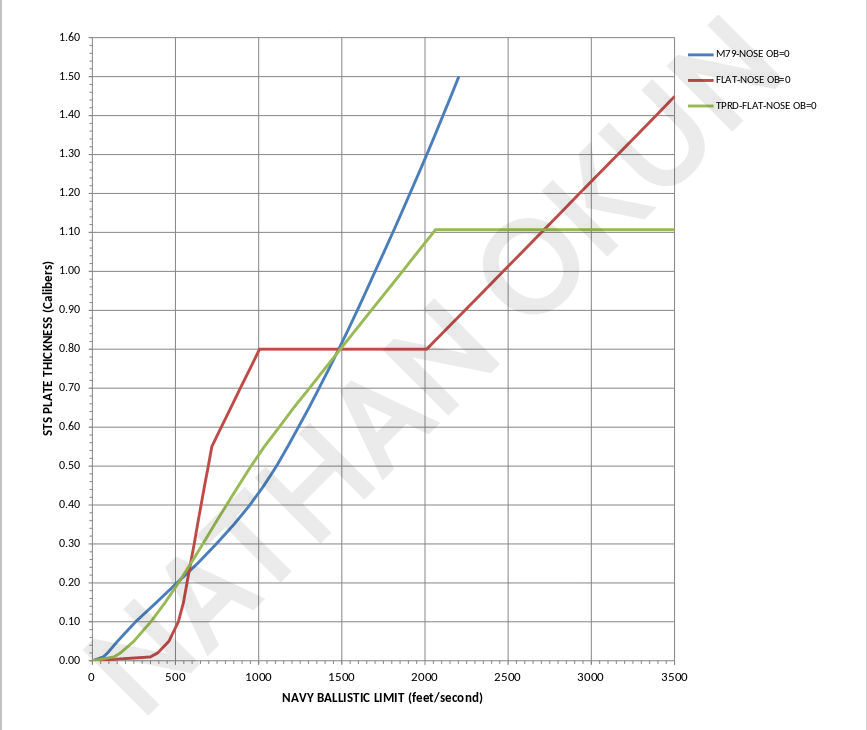
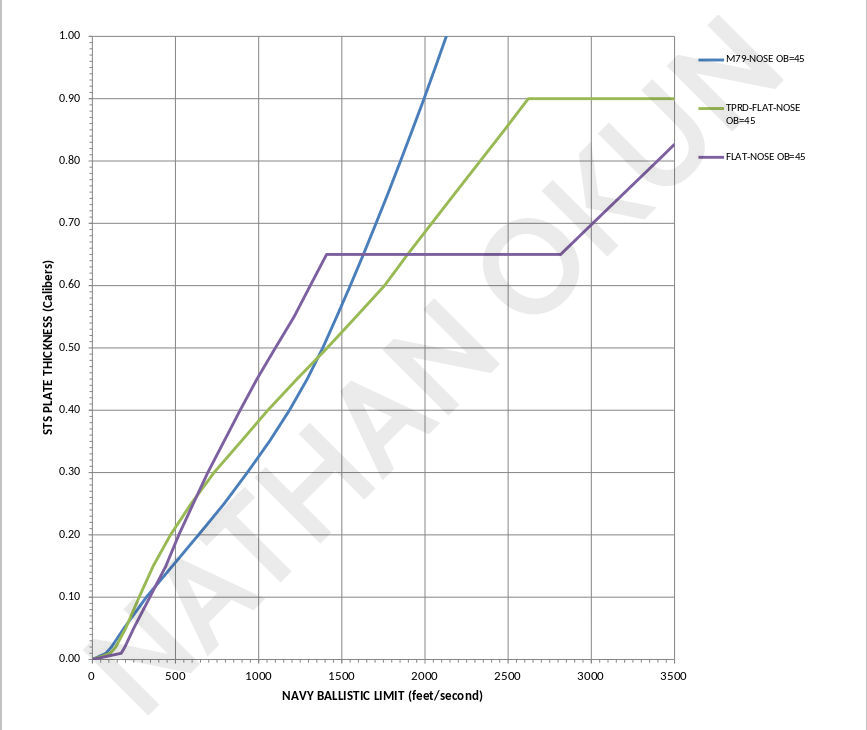
As the following diagrams show, up to 45 degrees obliquity, the M79-type blunt-point and tapered-flat-nose projectiles act very much alike for thin and intermediate plate thicknesses, with their penetration curves intertwining like a strand of DNA. It seems that the bending open of the ring of metal surrounding the tapered flat disk punched out of the armor takes so much force that it makes the bending open of the center portion with the blunt-point nose of rather little difference from punching out that center with the tapered flat portion. The two curves diverge when the tapered-flat-nose shatters against thicker plates or when higher obliquity allows the sharp corner of the tapered-flat-nose to cut into the plate and improve its penetration compared to a point which has its impact footprint enlarged and thus has degraded penetration due to glancing effects.
Until the full-flat-nose projectile shatters against thicker plates, it is superior from 0.2-caliber plate thickness and up to either of the other projectile types, though only slightly so for the middle obliquities around 45 degrees. While slicing out only the center region does not gain the projectile much from 0-45-or-so degrees obliquity, slicing out **all** of the plate material in front of the projectile with a full-width flat nose greatly reduces the resistance where otherwise the sliced out metal would have to be bent back and outward around the edges to let the projectile go through, as with the other two nose shapes.
When softer, weaker metals are used than STS, so that the shatter thicknesses go up, flat nose shapes obviously are a good design, such as against wrought iron armor during the US Civil War where such flat-nosed chilled-cast-iron and steel-tipped cast iron "bolts" were the primary weapon against ironclads from the rifled cannons that could use them.
It is rather amazing how small a taper (a mere 15% loss in flat-nose width here) is needed to change the penetration effectiveness of a flat-nosed projectile to almost that of a pointed nose over most of the range of plate thicknesses and obliquities likely to be met in a battle.
During the various tests, against plates that did not shatter the projectile at the NBL, increasing the striking velocity to much higher values, well above those that would have been needed to penetrate the thicker plates if those thicker plates did not cause shatter, had no effect on the projectiles. This means that the form of "shatter" occurring here is a compression of the nose as it is abruptly decelerated on impact and it is crushed between the plate and the lower projectile body. The nose is squeezed like horseshoe being made by a blacksmith between his hammer (the lower body) and his anvil (the plate hit). The more usual shock-wave-induced shatter, such as when hitting a high-quality face-hardened plate with an uncapped projectile, where the projectile shatters like brittle glass on impact, would have also caused shatter against the thinner plates when the striking velocity was raised to the point that the thicker plates were shattering the same projectiles at the same obliquity angle, since, except for some of the thinner plates, all plates hit here are rigid enough to cause shock-wave-induced shatter when the striking velocity is raised high enough. Though plate-thickness-dependent here instead of impact-velocity-dependent, once shatter sets in, increasing the striking velocity does not cure it, as can happen when the damage is caused by some other mechanism during the impact (base slap, middle-body collapse which I call "rupture", and so forth).
When the 3" flat-nosed projectiles were tested against STS against plates just under the thickness that shattered them, some of the projectiles had their front portion flatten slightly (termed "mushrooming"), dropping their penetration ability - that is, raising the NBL - slightly. Softer projectiles would do this to a greater extent, increasing the NBL gradually as plate thickness went up above and beyond the value with a non-deformed projectile, though shatter would suddenly set in much like it does for the stronger projectiles at the shatter thickness, as a step function there.

This article is copyrighted 2012 by Nathan Okun and is reproduced on NavWeaps.com with permission.
- 28 March 2012
- Benchmark.
