At its simplest, the drag force acting on a shell, or any other object
flying through the atmosphere (or water, or glue, or any other fluid for
that matter) is:
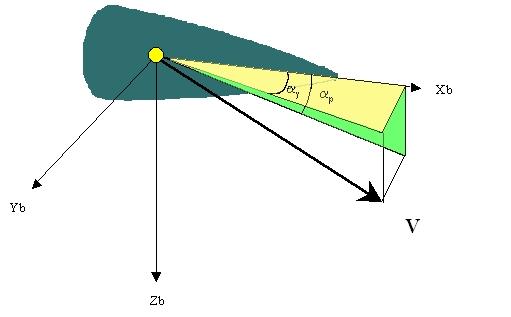
Cd is a dimensionless parameter that represents the drag acting on the shell for a specific flight condition. Common flight conditions include Mach number or velocity, altitude, and angle of attack Angle of attack, a is the angle between the body centerline axis and the prevailing wind. (Figure 1.)
Determination of Cd is the most difficult part of this procedure. It is highly variable, but is most dependent on the shape of the object, i.e. a streamlined object will have a lower Cd then a blunt one. Many methods exist for calculating Cd, but they are all one of 3 general methods:
- Experimental (wind tunnel)
- Theoretical (simplified calculations)
- Numerical (Computational fluid dynamics, or CFD.
The most straightforward method is 'a' Using a wind tunnel.
this involves solving equation 1 for Cd, then placing a model of the shell
in a wind tunnel with rho, S, and V already known. We can then measure
the force acting on the device that holds the model (the "sting") and calculate
Cd via:
Several other wind tunnel methods exist, but they all rely on the same premise; known tunnel conditions and model geometry. The advantage of this approach is that is probably the most realistic. The downsides to wind tunnel experiments are:
- wind tunnels are expensive
- scaling problems occur if the model is not full size
- interference from the tunnel walls
- measurement difficulties
In theoretical methods, simplifying assumptions are made in order to make the problem more solvable. These can involve simplifying the geometry and simplifying the equations. The full equation describing the flow of a fluid around a body are collectively known as the Navier Stokes Equations. These partial differential equations encompass the momentum, energy, and continuity equations of fluid flow. They are unsolvable in a closed form manner ( i.e. plug in what you know, crunch the numbers, and out spits the answer) But they can be simplified for specific geometries or flight conditions. The advantage to this approach is that it can yield a clean formula allowing plug and chug calculations. The con is that is restricted to simple geometries and physics, and usually can only be used on linear problems.
Numerical methods are fairly new, only having really been in use since the advent of the digital computer during WWII. Even after the first computers, the calculations proved to be so intensive that even in the mid 80's CFD often required the most advanced supercomputers available. Advanced CFD codes numerically solve the Navier Stokes equations and can produce complete flow fields around an object for a specific flight condition. Less complex problems and geometries can be analyzed using subsets of the NS equations or by making some simplifying assumptions. A common version includes CFD codes that solve the Euler equations. These are the NS equations with friction terms removed, but they are only usable above Mach 1. Otherwise several mathematical assumptions are violated and the codes will not run. CFD codes can solve time dependent problems, such as the flow around a shell as it travels down and leaves a gun barrel. The advantages of this approach are unrestricted geometry, complicated physics modeling, and time evolution of the flow. The cons are:
- computer round-off errors
- Boundary condition problems (initial conditions must be defined very accurately)
- Computer costs and run time.
Several 'combination' methods exist. These involve compilations of empirical and wind tunnel data combined with computer models of theoretical equations. These can yield acceptable results at a fairly low cost and computer speed. The downside to these methods are that they often require simplification of the geometry, and they include simplification of the physics. Examples of these include Missile DATCOM, the NSWC Aero Prediction Code, and several other variations on the methodology.
Many parameters can affect the final Cd. Altitude, surface roughness, spin, and nose bluntness are just a few that can influence Cd, and should be accounted for if maximum fidelity is desired.
Once all is said and done, Cd for a streamlined projectile can range from .18 up to .3 at Mach 2. As Mach increases, Cd will generally drop, and Cd will be much higher around Mach 1, due to transonic effect such as shock wave interactions.
Accurate kinematic prediction of a ballistic object requires that several initial conditions be known. Velocity, altitude, and angle of flight (commonly called flight path angle, or gamma) Also to be considered is the change in atmospheric density as altitude increases. At higher altitudes, density is lower with the net effect of less drag force acting on the shell. Many atmospheric models exist in both digital and tabular form. My personal favorite is the U.S. Standard Atmosphere, version 1962. These can easily be found in tech libraries or in an aerodynamics book.
What keeps the pointy end of the shell in front and the flat end at the back? Or, in other words, why is a shell stable in flight?
Several factors combine to keep a shell flying straight or tumbling:
The rifling of the barrel imparts a spin to the shell that results in a gyroscopic effect on the body. A gyro tends to maintain its orientation, so this assists the shell's stability. The equations of motion for a spinning object can be found in any Dynamics textbook, and generally require detailed knowledge of the objects mass properties.
Generally, the farther forward the center of gravity (cg) of a shell is, the more stable it will be. The cg is the point along the length of the where the same amount of weight is in front as in back. The point where it balances. Other mass properties of import are the moments of inertia of the shell. These are numerical representations of where the weight is located in an object and how it is distributed.
Unfortunately, shells tend to be statically unstable. This is due to their very shape. Pointy at the front, then a near constant diameter along the rest of their length. In flight, pressure builds up along the surface of an object. A surface more perpendicular to the line of flight tends to have a higher pressure, like when your hand is out a car window. Flat, it doesn't have much force on it, but if you turn it on its side then you can feel the increase in pressure. For a shell, this means that most of the force is toward the front, where the pointy end is. The point where this acts is called the center of pressure, or Xcp. Xcp is found by calculating the pressure distribution across the body, then integrating it. The resulting point where the resultant of all these forces lands is the center of pressure.
Of importance is that there is no force acting on the sides of the shell if it has no angle of attack. This means that it is pointing perfectly straight. If it has a slight angle, then the side that is exposed more to the airstream has a higher pressure, much like the hand out the window analogy.
For stability, think of the shell as a teeter totter with the pivot placed at the cg. If the Xcp is behind the cg, then if the shell takes on an angle of attack then it will have a tendency to correct itself. The aerodynamic force will try to straighten the shell out. If the Xcp is in front of the center of gravity, the tendency is for the angle of attack to get WORSE, causing the shell to tumble.
A good shell design will combine the aerodynamics, the mass properties, and the spin of the shell to permit the projectile to be pointy end forward for the entire flight. Unfortunately, the very shape of a shell contributes to instability. A WWII era shell generally had a windscreen on the front, and most of the weight concentrated towards the rear of the body. If no spin was imparted by rifling, the shell would tumble or stabilize at an angle of attack near 90. This is undesirable, since it means that the shell would be flying sideways (not good for range or penetration).
Recall that this is only a portion of the information needed to design a shell. Penetration and explosive power must also be addressed.
- 2 July 2000
- Updated.