One of the things I get asked about quite often is "what the heck is crh and how is it calculated." Nearly every time I have been asked that question, I've wound up expanding the definition in my "Definitions and Information" so that it is now one of the longest in those listings. However, even this explanation does not seem to be detailed enough, as I still get questions about it. So, here is a longer, more complete explanation.
Let's start with my Definition:
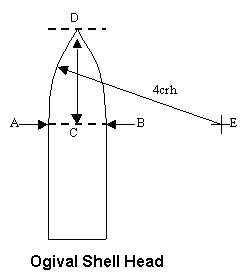
- crh
Caliber Radius Head. The pointed head of a projectile is described in terms of its ballistic length and the radius of the curvature of its nose. Larger numbers mean a more streamlined profile. Properly, crh is shown as a dual number such as 3/4crh, with the first number indicating the ballistic length and the second number indicating the radius of the curvature, but it is often abbreviated to a single number such as 4crh. In the sketch at the right, the dotted line between Points A and B is the "shoulder" which is the start point of the nose and the distance between these points is the caliber of the projectile. In this sketch, the radius of the curvature is from Point A to Point E and is four times the caliber of the projectile. The vertical distance between Points C and D is the ballistic length and is the most important factor in the design of a shell for stability in flight. In this sketch, the ballistic length is 4, as Point E is on the same plane as Points A and B. From these numbers, this projectile would properly be described as 4/4crh but this would normally be abbreviated to just 4crh. Shells of this general shape are described as being "ogival headed" and have superior ballistic performance. As can easily be imagined, a 6crh shell is more pointed and streamlined than is a 4crh shell. When crh is described as 5/10crh it means that the radius is 10 calibers long but the ballistic length is that of a 5crh shell. When a projectile is described as 5/∞crh it means that it has a ballistic length of 5 and its nose shape is conical (infinite radius), not ogival. Most USN projectiles had secant ogive ballistic nose shapes which were somewhat more conical than a simple tangent ogive (smooth merging joint with cylindrical lower-body side) and gave them a distinct "shoulder" where the nose met the cylindrical side of the lower body). This shape has slightly reduced air friction compared to a tangent ogive nose of the same length above the cylindrical body.
Now, if we move the center of the radius (Point E) downwards while keeping the radius constant, this will decrease the ballistic length of the projectile but keep the radius of the ogive the same.
Catch that? It's tricky.
Let's do a couple of mathematical and geometric examples working with the projectiles used for the famous British 15"/42 Mark I naval cannon.
The older British 15" projectiles commonly known as the "4crh" shells were really 3.05/4crh. Again, this meant that the ballistic length was 3.05 times the caliber while the ogive radius was 4 times the caliber. Some quick calculations with these numbers show that the ballistic length for this projectile was 45.75 inches and the ogive radius was 60 inches. To show how these numbers are used, we need to use a little basic geometry.
First, the length of a chord through a circle is determined by the following
geometric formula:
For crh calculations, h (height) is 0.5 * the caliber of the projectile
and R is the caliber of the projectile times the ballistic length multiplier.
And, as the ballistic length of a projectile is obviously only half of
the chord length, the "2" in the front of this above formula is eliminated.
This means that the ballistic length of a projectile can be calculated
using the values for crh as follows:
Referring to the sketch, let's use the above formula for an imaginary 15"
projectile with 4/4crh dimensions:
Now, as noted above, the British 4crh 15" projectile was actually 3.05/4crh.
Thus, the ballistic length of this projectile would be:
As the overall length of the British 3.05/4crh projectile was about 56", we can quickly calculate that the shoulder to base dimension of this projectile was 56" minus 25.1" equals 30.9". This base to shoulder dimension will be used in a subsequent calculation.
Now, let's turn our attention to the later British projectiles which were commonly known as the "6crh" shells. Now, how they came up with that designation is beyond me, as, unlike the "4crh" projectiles, there is no "6" in the actual crh values. Perhaps some trivia hunter looking though PRO files will enlighten me someday. Anyway, this projectile was actually 5/10crh. So, it had a ballistic length of 5 and an ogive radius of 10.
Determining the ballistic length with the formula above:
These numbers show that this projectile was about 7.5 inches longer than the older 4crh projectile. Assuming that the shell body for the 6crh projectile was roughly the same as that for the 4crh projectile, then its total length would be 32.7 inches + 30.9 inches = 63.6 inches. This turns out to be almost exactly the length of this projectile, thus confirming the accuracy of these calculations.
If you are still confused about what the crh values mean at this time, then my best suggestion is to get a compass - the drawing kind, not the magnetic kind - and start making curves. One of my correspondents on this matter used a mathcad program, ProE, and was able to teach himself how these values affect projectile design. But, assuming that all you have is a compass and a sheet of paper, let me give you an example.
Working with the dimensions for the 3.05/4crh 15" projectile, let's start by drawing a vertical rectangle representing the shell body. As calculated above, the shell body for this projectile was 15" x 30.9". Unless you have a really big piece of paper and some oversized drafting tools, this is difficult size to handle, so let's do a 1/10th scale drawing and make our vertical rectangle 1.5" x 3.1". Similar to the sketch above, label the corners at top end of the rectangle as Points A and B to denote the shoulder. As the 3.05 ballistic length of this projectile was calculated above as being 45.75 inches long, a 1/10th scale of this value would be about 4.6 inches.
Draw the following two curves lightly, as we will be erasing them in the next step. Using the compass, draw a curve with a radius of 4.6 inches starting at Point A with the center of the radius (Point E) precisely in line with the shoulder. Repeat this procedure on the opposite side of the rectangle and draw a curve starting at Point B, so that you now have two curves intersecting above the rectangle. Label this intersection as Point D. Your drawing should now look similar to the sketch above and represents a ballistic length of 3.05 and an ogive radius of 3.05.
Now, the next step is to give your projectile an ogive radius of 4. So, erase the two curves you have just drawn, but keep your Point D. As the ogive radius of this projectile was 4 times the caliber or 60 inches, a 1/10th scale value means that you should now set your compass to draw a 6 inch curve. Then, draw a curve that starts at Point A and ends at Point D. Note that in order to draw this curve correctly, you must move the center of the radius (Point E) downwards, below the shoulder line.
Repeat this procedure on the opposite side of the rectangle to finish the drawing.
You now have a 1/10th scale drawing of the 3.05/4crh projectile.
23 December 2004 - Updated
28 March 2019 - Added "Analytical Description of the Volume, Center of Gravity,
and Moments of Inertia for Tangent and Secant Ogives"

