This article discusses the formulation of an empirical formula for armor penetration used by William H. Garzke and Robert O. Dulin to generate armor penetration values for World War II battleship and battle cruiser main guns firing armor-piercing, capped (APC) shells against US homogeneous Class "B" armor. These values were published in a series of books on World War II battleships (Garzke and Dulin, 1976, 1980, 1985). The formula they used was reverse engineered from data gathered from the "NavWeaps" naval weapons website (DiGiulian, 1997). Least squares' fitting was used to determine the optimal exponents and scaling factor for the gun and shell parameters most important for armor penetration: the diameter of the shell (D), weight of the shell (W) and its velocity at impact (V), as well as a scaling factor. The derived formula is:

Penetration = (.0004689 x W^0.55 x V^1.1) / (D^0.65)

This simple equation fits the published data exceedingly well (±0.01").

Between 1976 and 1985 William H. Garzke and Robert O. Dulin published a series of books about battleships built or planned after the "battleship building holiday" imposed by the Washington Naval Treaty of 1922 and expiring at the end of 1936 (Garzke and Dulin, 1976, 1980, 1985). These books are highly detailed in their description of the design procedure, technical characteristics, operational histories, and damage analysis of these ships and include a thorough characterization of their guns: bore (shell diameter), shell types and weights, muzzle velocity, range and angle of fall as a function of elevation and of shell penetration of vertical (side) and horizontal (deck) armor as a function of range. These penetration values are often quoted and used to compare the armor penetration power of large naval guns and for computer modeling of ship-to-ship combat for World War II naval games. These penetration values are reported as being calculated using "a detailed US Navy empirical equation" against US homogeneous Class "B" armor, but the equation is not given, nor is there any reference to its exact formulation or origin.

Nathan Okun (2001) describes the USN empirical formula for armor penetration as being formulated by the United States Navy (USN) in the 1930s to calculate the penetration of armor piercing, capped (APC) shells fired by large naval guns against horizontal armor. It is derived from the Thompson all-purpose armor penetration formula (or "F-formula) of 1930 for penetration of APC shells against US Class "B" homogeneous chromium-nickel-steel armor, which is similar to US "Special Treatment Steel" (STS) armor. Mr. Okun has further developed the equation for use with cemented and face-hardened armor plate and to account for potential differences in the construction of individual shell types. Unfortunately, the published armor penetration values of Garzke and Dulin are not consistent with these equations; therefore an attempt was made to "reinvent" their equation by reverse engineering based on their published results.

An exhaustive search of Tony DiGiulian's "NavWeaps" website (1997) for World War II naval guns turned up 14 naval guns with penetration data from Garzke and Dulin's books at zero range and at zero obliquity (Table 1).

Ship	Country	Gun	D (inches)	W (pounds)	V (fps)	T (inches)
Yamato	Japan	46cm/45 Type 941	18.11	3219	2559	34.01
Iowa	USA	16"/50 Mk 7	16	2700	2500	32.62
S.Dakota	USA	16"/45 Mk 6	16	2700	2300	29.74
Colorado	USA	16"/45 Mk 5	16	2240	2520	29.68
Tennessee	USA	14"/50 Mk 7	14	1500	2700	28.03
Alaska	USA	12"/50 Mk 8	12	1140	2500	24.48
Littorio	Italy	381mm/50 M1934	15	1951	2789	32.07
H-Class	Germany	40.6cm/52 SK C/34	16	2271	2657	31.7
Bismarck	Germany	38cm/52 SK C/34	14.96	1765	2690	29.23
Scharnhorst	Germany	28cm/54.5 SK C/34	11.14	727.5	2920	23.79
Richelieu	France	380mm/45 M1935	14.96	1949	2575	29.43
Dunkerque	France	330mm/50 M1931	12.99	1235	2854	28.08
Lion	UK	16"/45 Mk II	16	2375	24002	29.03
Vanguard	UK	15"/42 Mk I	15	1938	24002	27.1

There are also armor penetration values for the British 14"/45 Mk VII gun mounted in the King George V battleships, but the values quoted were "partly based upon the USN Empirical Formula for Armor Penetration and partly based upon official data" (DiGiulian, 2013). These values were not included since they do not appear to have been derived solely from the Garzke and Dulin formula.

"Maximum thickness", although never defined by Garzke and Dulin, is assumed to mean the maximum thickness of armor that the shell can penetrate and still be capable of full detonation.

The best discussion of the USN empirical formula is from Nathan Okun's exhaustive article on historical penetration formulae (Okun, 2001), which states that the USN empirical formula is derived from the Thompson all-purpose armor penetration formula (or "F-formula) of 1930:

T/D = (1728.04)(W/D³)[(V/F)Cos(Ob)]²

Ignoring the Cos(Ob) term, since Ob =0°, and merging the 1728.04 scaling term with the F term since the results are all against the same armor with the same F, gives a general scaling term "s" and the formula becomes:

T/D = s(W/D³)V²

Since the interest is in the actual penetration value T, rather than the T/D ratio, multiplying both side of the equation by D gives:

T = s(W/D²)V²

To determine the value of the scaling constant "s" for a particular make of armor, one needs only to rearrange the equation for "s":

s = TD²/(WV²)

and plug in the maximum penetration values for the guns listed in Table 1 and their ballistic characteristics. If this is the same formulation as for the Garzke and Dulin penetration formula, then "s" should be the same for all guns against the same US Class B homogeneous armor.

Ship	Gun	D (inches)	W (pounds)	V (fps)	T (inches)	s (x107)	T (calc.)	Diff
Yamato	46cm/45 Type 94	18.11	3219	2559	34.01	5.2915	32.72	1.29
Iowa	16"/50 Mk 7	16	2700	2500	32.62	4.9486	33.56	0.94
S.Dakota	16"/45 Mk 6	16	2700	2300	29.74	5.3304	28.4	1.34
Colorado	16"/45 Mk 5	16	2240	2520	29.68	5.3414	28.29	1.39
Tennessee	14"/50 Mk 7	14	1500	2700	28.03	5.0241	28.4	0.37
Alaska	12"/50 Mk 8	12	1140	2500	24.48	4.9475	25.19	0.71
Littorio	381mm/50 M1934	15	1951	2789	32.07	4.7547	34.34	2.27
H-Class	40.6cm/52 SK C/34	16	2271	2657	31.7	5.0523	31.96	0.24
Bismarck	38cm/52 SK C/34	14.96	1765	2690	29.23	5.1249	29.04	0.19
Scharnhorst	28cm/54.5 SK C/34	11.14	727.5	2920	23.79	4.7596	25.45	1.66
Richelieu	380mm/45 M1935	14.96	1949	2575	29.43	5.0967	29.4	0.03
Dunkerque	330mm/50 M1931	12.99	1235	2854	28.08	4.7102	30.35	2.27
Lion	16"/45 Mk II	16	2375	2400	29.03	5.4325	27.2	1.83
Vanguard	15"/42 Mk I	15	1938	2400	27.1	5.4563	25.26	1.81

The values for "s" vary a bit ( ca. 5%) and consequently, the values for T(calc.), calculated with the average value of "s", also vary somewhat from the published values. The root mean square deviation (RMSD) across all 14 guns is 1.38". Since both the published values and those determined here are calculated results, ostensibly with the same formula, these results are rather disappointing (Fig. 1).

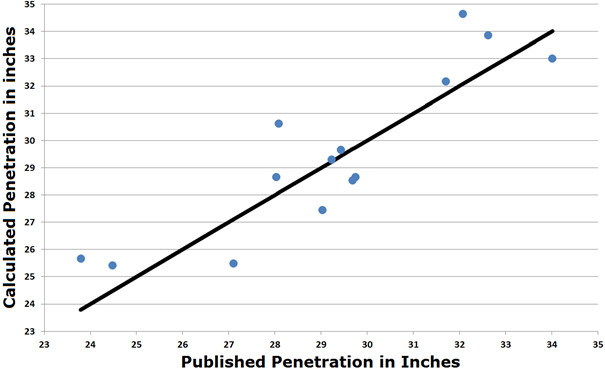
The Thompson formula was derived from the physics of a high speed projectile striking armor plate, but the USN empirical formula was, derived empirically, i.e. collecting data from controlled firings of large naval guns at armor plates and determining the equation that best fits the measured data (Okun, 2001). In addition using firing tests to empirically evaluate the "F" values for different makes of armor, the exponents for "D", "W", and "V" themselves were found to vary according to armor type. For example, against face-hardened armor plate the exponent for "W" drops to 0.2, while that for "V" drops to 1.21 (Okun, 2016). Using the published data from the empirical formula used by Garzke and Dulin (Table 1), it might be possible to "reverse engineer" their equation. In addition to searching for an optimal scaling factor "s" , the optimal exponents for W, D, and V would also have to be determined. The general equation would therefore be:

T = sW^aD^bV^c

Least squares (see >Appendix) is a powerful technique for optimizing parameters against observed data, but works better for summations than multiplicative formulas, so the obvious solution is to take the logarithm of both sides of the equation in order to recast it as a summation:

log(T) = log(s) + a*log(W) + b*log(D) + c*log(V)

Least squares fitting the above data to this equation (Priestle, 2016) gave the following values for a, b, c and "s":

T = (0.000469) x W0.5506 x D-0.6521 x V1.1001

Using this equation gave the following results for estimating armor penetration:

Ship	Gun	D (inches)	W (pounds)	V (fps)	T (inches)	T (calc.)	abs(diff)
Yamato	46cm/45 Type 94	18.11	3219	2559	34.01	34.00	0.01
Iowa	16"/50 Mk 7	16	2700	2500	32.62	32.61	0.01
Littorio	381mm/50 M1934	15	1951	2789	32.07	32.08	0.01
H-Class	40.6cm/52 SK C/34	16	2271	2657	31.70	31.70	0.00
S.Dakota	16"/45 Mk 6	16	2700	2300	29.74	29.75	0.01
Colorado	16"/45 Mk 5	16	2240	2520	29.68	29.68	0.00
Richelieu	380mm/45 M1935	14.96	1949	2575	29.43	29.42	0.01
Bismarck	38cm/52 SK C/34	14.96	1765	2690	29.23	29.22	0.01
Lion	16"/45 Mk II	16	2375	2400	29.03	29.05	0.02
Dunkerque	330mm/50 M1931	12.99	1235	2854	28.08	28.09	0.01
Tennessee	14"/50 Mk 7	14	1500	2700	28.03	28.02	0.01
Q. Elizabeth	15"/42 Mk I	15	1938	2400	27.10	27.09	0.01
Alaska	12"/50 Mk 8	12	1140	2500	24.48	24.47	0.01
Scharnhorst	28cm/54.5 SK C/34	11.14	727.5	2920	23.79	23.80	0.01

The root mean square deviation for the 14 guns has now dropped to 0.011", essentially to the accuracy of the published penetration values, which were typically reported to the nearest 1/100th of an inch. Not surprisingly, plotting the original Garzke and Dulin published penetration values against the values calculated from the formula above (equation 1) gives essentially coincident lines (Fig. 2).

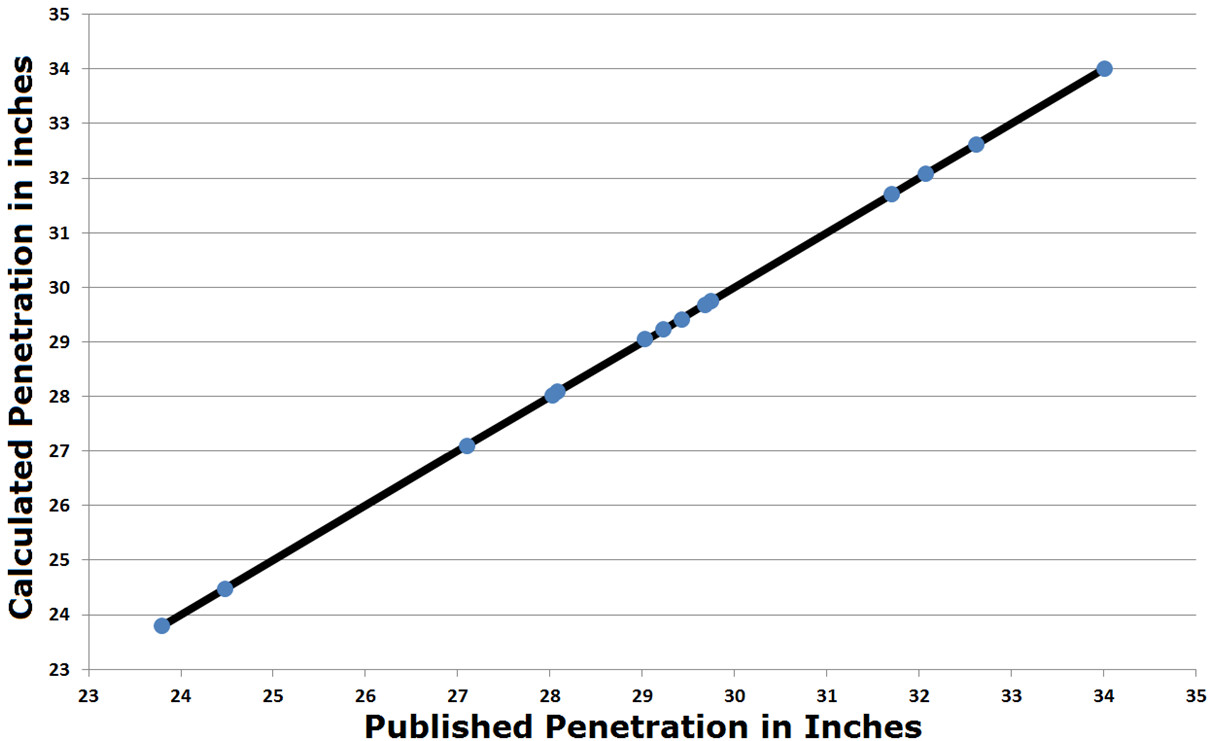
This astonishing accuracy is only possible because both sets of data are of calculated values and are not being fitted to real-world measurements, although the Garzke and Dulin formula itself was certainly derived from measured data. More published values would help validate this formula, since they weren't used to generate it. As it currently is, determining 4 values from 14 data points give an observation to variable ratio of 3.5:1, which , while well over-determined (> 1:1), is still rather low.

It is interesting to note that the exponents of T, W, and D are, to the first 2 digits, evenly divisible by 5, and that the 3rd and 4th digits are rather small: "06", "21", and "01":

T = (0.000469) x W^0.5506 x D^-0.6521 x V^1.1001

Might it not be that the original exponents were actually 0.55, -0.65 and 1.10, respectively? Calculating exponents in the 1930s and 1940s was far more difficult and time-consuming than today. Would trimming off the last two digits, possibly with some compensation in the scaling factor, still give acceptable results, i.e. differences in the 0.01" range?

Setting the exponents to 0.55, -0.65 and 1.10, recalculating the penetration values and then scaling them as was done in Table 2 gave a scaling factor of 0.0004689, giving:

T = (0.0004689) x W^0.55 x D^-0.65 x V^1.1

It was found necessary to have 4 digits in the scaling factor, since the penetration values themselves have 4 digits. The RMSD between published and calculated values (Table 4) is 0.012", only marginally worse than using 4 digits in the exponents (Table 3).

Ship	Gun	D (inches)	W (pounds)	V (fps)	T (inches)	T (calc.)	abs(diff)
Yamato	46cm/45 Type 94	18.11	3219	2559	34.01	34.01	0.00
Iowa	16"/50 Mk 7	16	2700	2500	32.62	32.61	0.01
Littorio	381mm/50 M1934	15	1951	2789	32.07	32.08	0.01
H-Class	40.6cm/52 SK C/34	16	2271	2657	31.7	31.71	0.01
S.Dakota	16"/45 Mk 6	16	2700	2300	29.74	29.75	0.01
Colorado	16"/45 Mk 5	16	2240	2520	29.68	29.69	0.01
Richelieu	380mm/45 M1935	14.96	1949	2575	29.43	29.42	0.01
Bismarck	38cm/52 SK C/34	14.96	1765	2690	29.23	29.23	0.00
Lion	16"/45 Mk II	16	2375	2400	29.03	29.06	0.03
Dunkerque	330mm/50 M1931	12.99	1235	2854	28.08	28.10	0.02
Tennessee	14"/50 Mk 7	14	1500	2700	28.03	28.02	0.01
Q. Elizabeth	15"/42 Mk I	15	1938	2400	27.1	27.10	0.00
Alaska	12"/50 Mk 8	12	1140	2500	24.48	24.47	0.01
Scharnhorst	28cm/54.5 SK C/34	11.14	727.5	2920	23.79	23.80	0.01

It has proven possible to reverse engineer the empirical formula for calculating the oft-quoted armor penetration values of Garzke and Dulin for large caliber guns. The formula is simple and the results are dependent on only three characteristics of the gun's shells in question: its diameter, its total weight and its muzzle velocity. These results are only valid for armor-piercing, capped (APC) shells.

Another interesting observation is that, given that shell weights increase roughly with the cube of the shell diameter, this means that for a given velocity, penetration increases linearly with shell diameter:

Penetration α W^0.55 / D^0.65 = D^3x0.55 / D^0.65

= D^1.65 / D^0.65

= D^1.0

In other words, for a constant velocity, penetration is linearly proportional to the diameter of the shell, which agrees with the rule-of-thumb that the thickness of a battleship's side armor should be the same as the bore diameter of its main guns. It also explains how this simple formula can fit the penetration data of guns whose bores run from 11.1" to 18.1" and might even offer some hope of being valid for smaller caliber guns, but again, only for APC shells. It also predicts that higher-than-average penetration for a given diameter shell can be achieved either by heavier shells for that diameter, but at the cost of a much smaller burster charge (the American approach in WWII), or by higher muzzle velocities, but at the cost of wearing out the guns too quickly (the German, French, and Italian approach).

Lundgren and Worth (2009), using the FACEHARD program of Nathan Okun (2001), have calculated and tabulated penetration of face-hardened side armor from five WWII belligerents (Great Britain, the United States, Italy, Germany, and Japan) for naval guns from these nations, plus France, at various ranges, but always with zero obliquity (shell impacting perpendicular to the face of the armor). Most of the guns are from battleship or battle cruisers, although a few are from heavy and light cruisers. For the comparison to the results from the Garzke and Dulin empirical formula, as formulated in this article (equation 2), only the FACEHARD penetration at range = 0 was used and only for "effective" penetration (complete penetration and the shell still able to detonate) against British side armor (this seems to be closest to the Garzke and Dulin results). In addition, only results with armor-piercing, capped shells were used.

The results from the Garzke and Dulin empirical formula and FACEHARD are displayed in Table 5 and plotted against the diameter of the APC shells in Figure 3.

Ship	Gun	D (inches)	W (pounds)	V (fps)	T(G&D)	T(FACEHARD)
Yamato	46cm/45 Type 94	18.11	3219	2559	34.01	31.7
Nagato	41cm/453rd Year Type	16.14	2249	2645	31.20	28.8
Iowa	16"/50 Mk 7	16	2700	2500	32.61	29.5
S.Dakota	16"/45 Mk 6	16	2700	2300	29.75	26.6
Lion	16"/45 Mk II	16	2375	24003	29.06	31.9
H-Class	40.6cm/52 SK C/34	16	2271	2657	31.71	30.0
Colorado	16"/45 Mk 5	16	2240	2520	29.69	29.9
Nelson	16"/45 Mk I	16	2048	2614	29.42	33.0
Littorio	381mm/50 M1934	15	1951	2789	32.08	31.9
Q. Elizabeth	15"/42 Mk I	15	1938	2458	27.70	30.6
Richelieu	380mm/45 M1935	14.96	1949	2575	29.42	32.9
Bismarck	38cm/52 SK C/34	14.96	1765	2690	29.23	31.1
KGV	14"/45 Mk VII	14	1590	2483	26.38	28.7
Tennessee	14"/50 Mk 7	14	1500	2700	28.02	28.1
Pennsylvania	14"/45 Mk 8	14	1500	2600	26.88	26.9
Kongo	14"/45 41st Year Type	14	1485	2543	26.09	23.6
Dunkerque	330mm/50 M1931	12.99	1235	2854	28.10	29.7
Cavour	320mm/44 M1934	12.6	1157	2723	26.26	25.7
Courbet	305mm/45 M1906	12.01	952	2569	22.82	12.3
Alaska	12"/50 Mk 8	12	1140	2500	24.47	24.0
Wyoming	12/50 Mk 7	12	870	2900	24.83	18.6
Scharnhorst	28cm/54.5 SK C/34	11.14	727.5	2920	23.80	23.7
Lützow	28cm/52 SK C/28	11.14	661	2986	23.14	19.5
Baltimore	8"/55 Mk 12	8	335	2500	16.24	14.9
Jap CAs	20cm/50 3rd Year Type No. 2	8	277	2756	16.28	16.2
Prinz Eugen	20.3cm/60 SK C/34	8	269	3035	17.82	18.6
Pensacola	8"/55 Mk 9	8	260	2800	16.00	16.2
Oyodo	15.5cm/60 3rd Year Type	6.1	123	3018	13.73	13.7
Cleveland	6"/47 Mk 16	6	130	2500	11.63	10.5
Königsberg	15cm/60 SK C/25	5.87	100.3	3150	13.19	10.3
Ger. BBs/BCs	15cm/55 SK C/28	5.87	99.8	2871	11.88	9.2

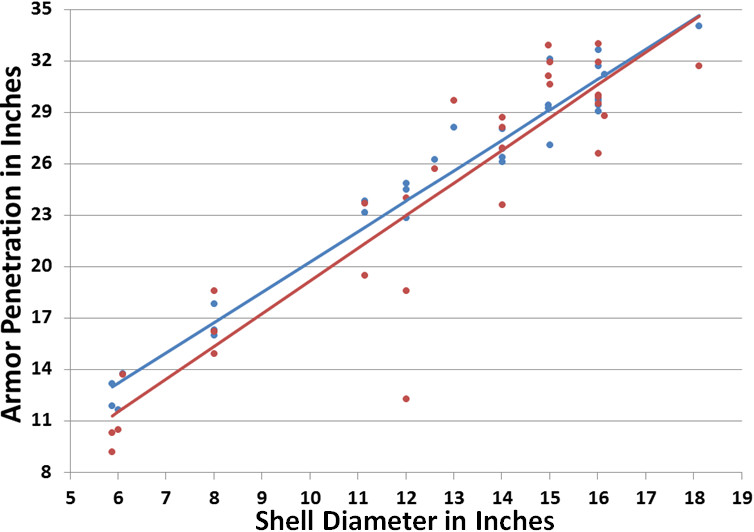
The Garzke and Dulin values scatter much less from their best fit line than those from FACEHARD (RMSD = 1.25" vs. 3.03"), possibly because the Garzke and Dulin formula has only three variables and two of them are highly correlated (shell diameter and weight). FACEHARD takes far more parameters into account, e.g. shell construction (hardness, nose shape, fuzing, cap construction) and the armor itself, e.g. how deep the armor is "hardened", presence/absence of a "decapping" layer, etc. In addition, the Garzke and Dulin data is against US homogeneous Class B armor and the FACEHARD results are against British cemented armor. Despite these differences, the results are generally quite similar with an overall correlation of 0.9253 with the FACEHARD values being, on average, about 3% smaller. The RMSD between the values is rather large, 3.00", but much of this is due to the differences for the French 12" gun mounted in the old Courbet-class battleships, predicted to penetrate almost 23" of armor by the Garzke and Dulin formula and just a bit over 12" with FACEHARD. Removing this single discrepancy brings the RMSD down to 2.3". I've not found any explanation of, or even allusion to, very poor penetration of the French 12" gun in the literature, roughly half of what one would expect.

Table 6 gives the "Top Ten" guns ordered by penetration, as determined by the Garzke and Dulin empirical formula and by FACEHARD. Although the two formulas give quite similar results, the rank orderings do show some interesting differences:

G&D Empirical Formula

Rank	Ship	Gun	Pene
1	Yamato	46cm/45 Type 94	34.01
2	Iowa	16"/50 Mk 7	32.61
3	Littorio	381mm/50 M1934	32.08
4	H-Class	40.6cm/52 SK C/34	31.71
5	Nagato	41cm/453rd Year Type	31.20
6	S.Dakota	16"/45 Mk 6	29.75
7	Colorado	16"/45 Mk 5	29.69
8	Nelson	16"/45 Mk I	29.42
9	Richelieu	380mm/45 M1935	29.42
10	Bismarck	38cm/52 SK C/34	29.23

FACEHARD

Rank	Ship	Gun	Pene
1	Nelson	16"/45 Mk I	33.0
2	Richelieu	380mm/45 M1935	32.9
3	Lion	16"/45 Mk II	31.9
4	Littorio	381mm/50 M1934	31.9
5	Yamato	46cm/45 Type 94	31.7
6	Bismarck	38cm/52 SK C/34	31.1
7	Q. Elizabeth	15"/42 Mk I	30.6
8	H-Class	40.6cm/52 SK C/34	30.0
9	Colorado	16"/45 Mk 5	29.9
10	Dunkerque	330mm/50 M1931	29.7

The rankings from the Garzke and Dulin empirical formula seem to be dominated by the size (caliber) of the gun, with only the guns of 15" or larger being listed and, except for the Italian 15" gun, are strictly ranked by gun caliber. The rankings by FACEHARD are also dominated by the largest-caliber guns, but also includes the 13" guns of the French Dunkerque class battle cruisers. The Garzke and Dulin list includes the guns of the Iowa, Nagato, and South Dakota (all 16"ers.) that are replaced by the guns from the Lion (16"), the Queen Elizabeth (15"), and the Dunkerque (13") in the FACEHARD list.

Due to the popularity of the three "battleship books" by William H. Garzke and Robert O. Dulin (1976, 1980, 1985) among naval enthusiasts, the armor penetration values they published in these books have become very known within the naval gunnery / warship community and have been used for modeling ship to ship combat in a number of naval wargames. Unfortunately, Garzke and Dulin do not provide the exact formula they used to calculate these values, nor do they reference the origin of this formula. Tantalizingly, they state that the penetration values were calculated with "a detailed US Navy empirical equation" (Garzke and Dulin, 1975, p. 308 [1995 revised version]; 1980, p. 373; 1985, p. 501). Their values do not fit the USN Empirical Formula for Armor Penetration, derived from the Thompson all-purpose armor penetration formula (or "F-formula) of 1930. An attempt to reverse engineer their equation from their published values using least squares was successful, leading to a simple equation that generates the published values with surprising accuracy.

Least squares [see Weisstein (2016) for a detailed introduction to this subject] is a technique for finding the best parameter values in an equation that fit the observed (measured) data. More precisely, it finds those values that minimize the sum of the squares of the differences between observed and calculated values. It is probably best known for its use in fitting a best straight line through a set of point that are approximately linear, for example, the "SLOPE" and "INTERCEPT" functions in Microsoft's Excel spreadsheet program.

The advantage of the least squares technique is that it gives the absolutely best parameters that fit the data. One weakness of the method is that, since it minimizes based on the square of the differences between observed and calculated values, it is very sensitive to outliers (potentially bad data), that, if really due to a bad or spurious measurement or other error, can significantly degrade the results. This weakness can be overcome if the number of parameters to be fitted is small compared to the number of observations. Typically one would like to have at least 3x as many independent observations as parameters. The more high quality data one has, the easier it becomes to spot bad data. Another limitation is that reliability is only guaranteed within the boundaries of the input data, in this case, only for guns firing APC shells with diameters between 11.1" and 18.1". Extrapolations outside of these limits can be made, of course, but there is no real data to support this.

An Excel spreadsheet for using least squares for determining the values for an equation with three parameters and a constant term is available from the author (Priestle, 2016).

• ^The official designation for this gun was actually "40cm/45 Type 94" as part of the Japanese effort to hide its true size.
• ^2.12.2Most of the MV values in this table are for "new gun" data, but for these two UK guns Garzke and Dulin chose to use "average gun" values.
• ^Although the published MV for this gun is 2450fps, Lundgren and Worth use 2400fps.

• DiGiulian, Tony (1997): http://www.navweaps.com.
• DiGiulian, Tony (2013): http://www.navweaps.com/Weapons/WNBR_14-45_mk7.php
• Garzke Jr., William H. and Dulin, Robert O. (1976, revised 1995) United States Battleships, 1935-1992, pp. 308-317, United States Naval Institute, Annapolis, Maryland.
• Garzke Jr., William H. and Dulin, Robert O. (1980) Allied Battleships in World War II, pp. 374-375, United States Naval Institute, Annapolis, Maryland.
• Garzke Jr., William H. and Dulin, Robert O. (1985) Axis and Neutral Battleships in World War II, pp. 502-503, United States Naval Institute, Annapolis, Maryland.
• Lundgren, Richard and Worth, Richard (2009): http://www.navweaps.com/index_nathan/Penetration_index.php
• Okun, Nathan (2001): http://www.navweaps.com/index_nathan/Hstfrmla.php
• Okun, Nathan (2016) personal communication
• Priestle, John (2016) A Microsoft Excel spreadsheet with the raw input and calculations is available from the author (priestle@bman.ch). Unfortunately, it’s a German version of Excel and the function names may need translating.
• Weisstein, Eric W. (2016) "Least Squares Fitting." From MathWorld--A Wolfram Web
• Resource: http://mathworld.wolfram.com/LeastSquaresFitting.html

The author gratefully acknowledges detailed discussions about the USN Empirical Formula for Armor Penetration with Mr. Nathan Okun of Oak View, Calif., USA.

1 March 2016

New article.